Decay (hazma.decay)¶

In this section, we describe how the radiative decay spectra are computed for the muon, charged pion and neutral pion.

Functions¶

The submodule hazma.decay has the following functions:

Muon	hazma.decay.muon
Neutral Pion	hazma.decay.neutral_pion
Charged Pion	hazma.decay.charged_pion
Short Kaon	hazma.decay.short_kaon
Long Kaon	hazma.decay.long_kaon
Charged Kaon	hazma.decay.charged_kaon

Details¶

Muon¶

The dominant contribution to the radiative decay of the muon comes from \(\mu^{\pm}\to e^{\pm}\nu\bar{\nu}\gamma\). The unpolarized differential branching fraction of this decay mode in the muon rest frame can be written as [1]

\[\dfrac{dB}{dy \ d\cos\theta_{\gamma}^{R}} = \dfrac{1}{y} \dfrac{\alpha}{72\pi}(1-y)\left[ 12\left(3 - 2y(1-y)^2\right)\log\left(\dfrac{1-y}{r}\right) + y(1-y)(46 - 55y) - 102\right]\]

where \(r = (m_{e}/m_{\mu})^2\), \(0 \leq y = 2E_{\gamma}^{R\mu}/m_{\mu} \leq 1 - r\), (\(E_{\gamma}^{R\mu}\) is the energy of the photon in the muon rest frame) and \(\theta_{\gamma}^{R}\) is the angle the photon makes with respect to some axis in the muon rest frame. In order to obtain the decay spectrum in the laboratory frame, we need to boost the above spectrum. In other words, we need to change variables from the gamma ray energy and angle in the muon rest frame to those in the lab frame. We then integrate over the angle to compute \(dN/dE_{\gamma}\). The Jacobian for this change of variables is

\[J = \dfrac{1}{2\gamma(1-\beta\cos\theta_{\gamma}^{L})}\]

where the boost parameters are

\[\gamma = E_{\mu} / m_{\mu}, \qquad \beta = \sqrt{1 - \left(\dfrac{m_{\mu}}{E_{\mu}}\right)^2}\]

Integrating over angles yields the gamma ray spectrum in the lab frame:

\[\dfrac{dN}{dE_{\gamma}^{L}} = \int_{-1}^{1}d\cos\theta_{\gamma}^{L} \dfrac{1}{2\gamma(1-\beta\cos\theta_{\gamma}^{L})} \dfrac{dB}{dE_{\gamma}^{R\mu}}\]

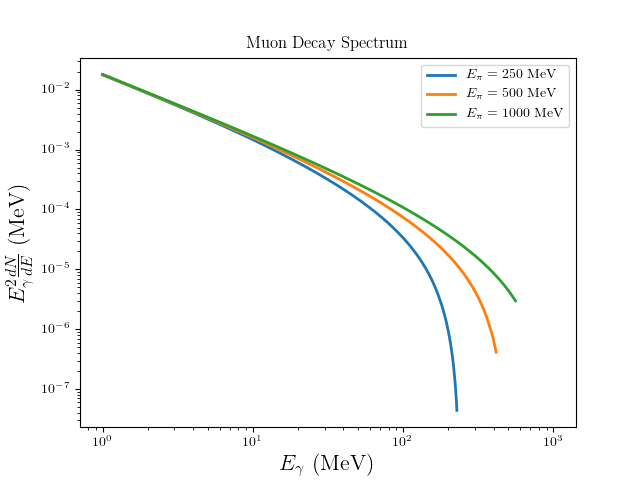
Gamma ray spectrum from radiative muon decay

Charged Pion¶

To compute the gamma ray spectrum from a charged pion, one considers to possible decay modes. These decay modes are \(\pi^{\pm} \to \mu^{\pm}\nu_{\mu}\gamma\) and \(\pi^{\pm} \to \mu^{\pm}\nu_{\mu} \to e^{\pm}\nu_{\mu}\nu_{\mu}\nu_{e}\gamma\). To compute the gamma ray spectrum from the first decay mode, one uses results from [2]. It turns out that the spectrum from this decay mode is roughly a factor of 100 times smaller than the spectrum from the second decay mode. We thus ignore the contributions from \(\pi^{\pm} \to \mu^{\pm}\nu_{\mu}\gamma\).

To compute the γ-ray spectrum from \(\pi^{\pm} \to \mu^{\pm}\nu_{\mu} \to e^{\pm}\nu_{\mu}\nu_{\mu}\nu_{e}\gamma\), we first take the muon decay spectra (see section on muon decay spectra) and boost the muon into the pion rest frame use the following:

\[\gamma_{1} = E_{R\mu}/m_{\mu} \qquad \beta_{1} = \sqrt{1-\left(\dfrac{m_{\mu}}{E_{R\mu}}\right)^2} \qquad E_{R\mu} = \dfrac{m_{\pi}^2 - m_{\mu}^2}{m_{\pi}^2 + m_{\mu}^2}\]

where \(E_{R\mu}\) is the energy of the muon in the pion rest frame. The photon spectrum in the charged pion rest frame, \(dN/dE_{\gamma}^{R\pi}\), is obtain by integrating the differential branching ratio times a Jacobian factor \(1/2\gamma_{1}(1-\beta_{1}\cos\theta_{\gamma}^{R\pi})\) over the angle the photon makes with the muon. Once this integration is completed, one then boosts into the laboratory frame of reference. The steps are nearly identical to boosting from the muon rest frame to the pion rest frame. The only thing that changes in the boost factor and the Jacobian. In going from the charged pion rest frame to the laboratory frame, the Jacobian and boost factor are

\[J = \dfrac{1}{2\gamma_{2}(1-\beta_{2}\cos\theta_{\gamma}^{L})} \qquad \gamma_{2} = E_{\pi} / m_{\pi} \qquad \beta_{2} = \sqrt{1 - \left(\dfrac{m_{\mu}}{E_{\pi}}\right)^2}\]

The gamma-ray spectrum in the laboratory frame will thus be

\[\dfrac{dN}{dE_{\gamma}^{L}} = \int_{-1}^{1} d\cos\theta_{\gamma}^{L} \dfrac{1}{2\gamma_{2}(1-\beta_{2}\cos\theta_{\gamma}^{L})} \times \left(\int_{-1}^{1}d\cos\theta_{\gamma}^{R\pi} \dfrac{1}{2\gamma_{1}(1-\beta_{1}\cos\theta_{\gamma}^{L})} \dfrac{dB}{dE_{\gamma}^{R\mu}} \right)\]

where

\[E_{\gamma}^{R\mu} = \gamma_{1} E_{\gamma}^{R\pi}\left(1 - \beta_{1}\cos\theta_{\gamma}^{R\pi}\right)\]

and

\[E_{\gamma}^{R\pi} = \gamma_{2} E_{\gamma}^{L}\left(1 - \beta_{2}\cos\theta_{\gamma}^{L}\right)\]

The limits on the photon energy are given by

\[0 \leq E_{\gamma}^{L} \leq \dfrac{m_{\mu}^2 - m_{e}^2}{2m_{\mu}} \gamma_{1}\gamma_{2}(1+\beta_{1})(1+\beta_{2})\]

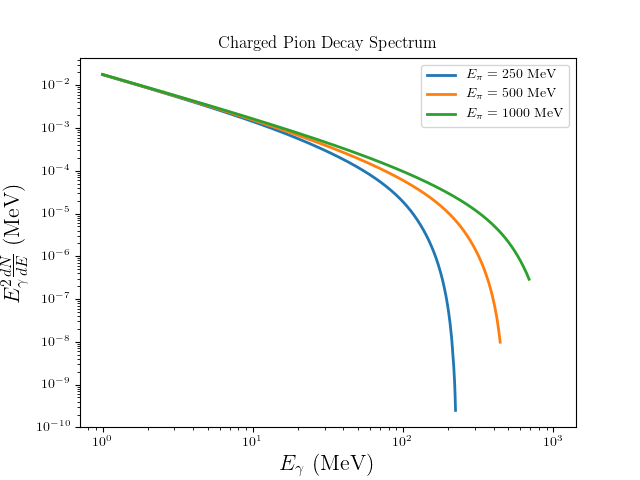
Neutral Pion¶

The dominant decay mode of the neutral pion is \(\pi^{0}\to\gamma\gamma\). In the laboratory frame, the spectrum is

\[\dfrac{dN}{dE_{\gamma}} = \dfrac{2}{m_{\pi}\gamma\beta}\]

References¶

[1]	Kuno and Y. Okada, Reviews of Modern Physics 73, 151 (2001), ISSN 00346861.

[2]	Olive, P. D. Group, et al., Chinese physics C 38, 090001 (2014).